算数 組み合わせ 何通り 599221-算数 組み合わせ 何通り
Kamakura Ed Jp
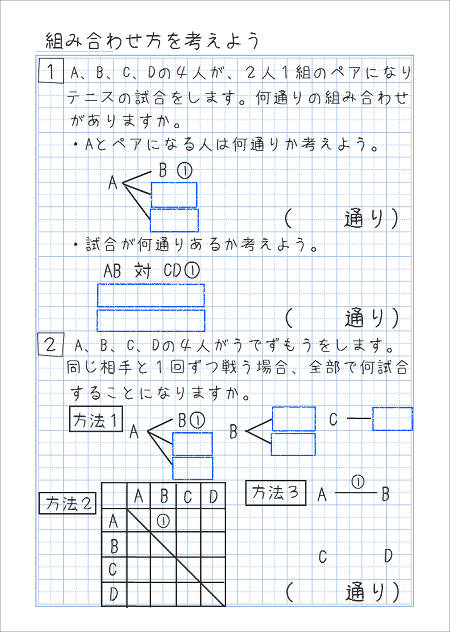
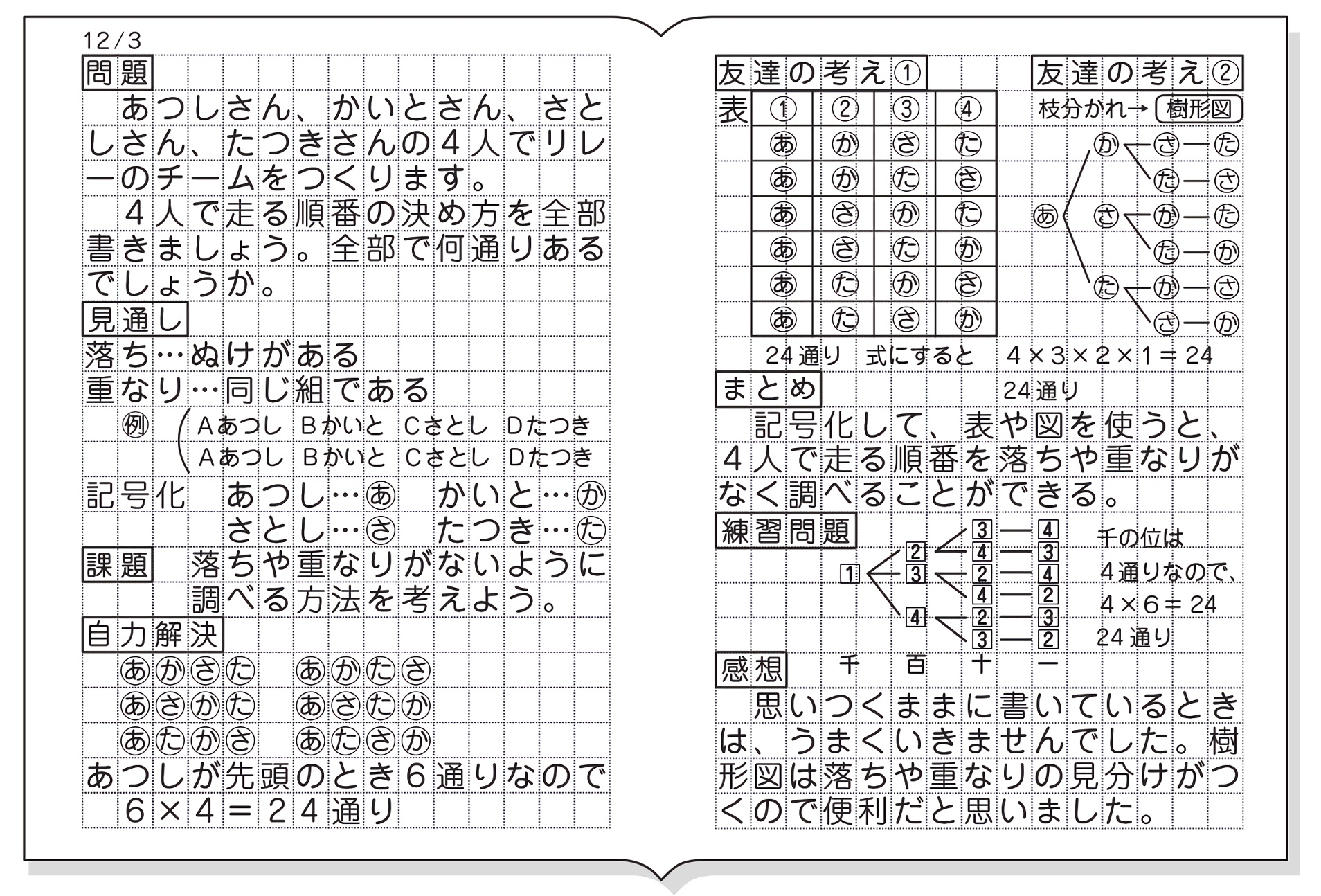
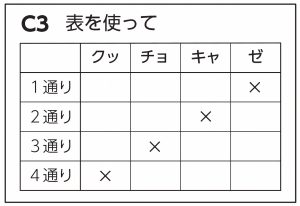
(2)100円硬貨2枚,50円硬貨2枚,10円硬貨3枚の全部,または一部・・・何通りありますか。 (3) 6枚の100円硬貨をAさん,Bさん・・・で分ける方法は全部で何通りありますか。 <組み合わせの問題の解説 pdf> 赤玉が3個,青玉か2個ご白玉が1個あります。 1、2、3、4のカードを使ってつくれる3けたの整数は何通りありますか。 解法 1から始まるものを必ず順番に書く 123 124 132 134 142 143 他のカードが先頭の時にも6通りずつあるので6×4=24通り 計算のみ解法 100の位が4通り 10の位がそのそれぞれに対して3通り
算数 組み合わせ 何通り
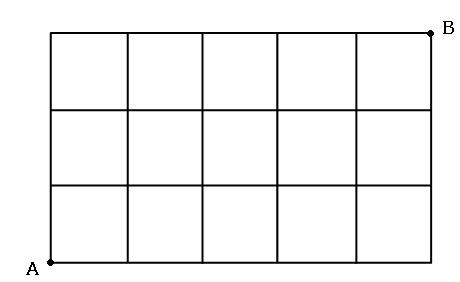
算数 組み合わせ 何通り-中学受験算数解法1000→「イメージでわかる中学受験算数」 《図 1》は一辺の長さが1の立方体を4個組み合わせて、 《図1》、《図2》のそれぞれについて何通りありますか。 解法例 図のように、各頂点での道順の場合の数を記入していくと、 図1はA地点からB地点へ,遠回りせずに行く限り,どの順路も東向きに4回,北向きに3回移動していることが分かります 東に移動することをe (eastの略),北に移動することをn (northの略)で表すと,右の茶色の順路はeneenenに対応しており,青の順路はnneeneeに対応して

ならべ方 と 組み合わせ 小学校の 場合の数 の問題の解き方 数学fun
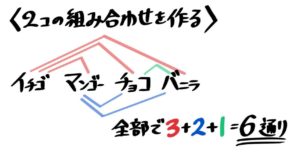
全部で何通りあるでしょう。 (2) バニラ,チョコ,ストロベリー,抹茶,グレープの5種類のアイスクリームの中から2種類を選びます。アイスクリームの組み合わせは全部で何通りあるでしょう。 式不要。正解は,(1)は「18(通り)」,(2)は「10(通り)」。組合せ キャラが7人いる漫画で複数人が単行本の表紙になるとき表紙は何巻まで新しい組み合わせを出せるか調べるため。 ゆゆ式は799巻まで続く。 使いやすく助かりました。 ゲームのアイテムに69種類の効果のうち3つがランダムでつくというものがあり COMBIN 組み合わせの数を求める 対応バージョン: 365 19 16 13 10 総数個の項目のなかから抜き取り数個を取り出したとき、何種類の組み合わせが可能であるかを求めます。 二項係数を求めることもできます。
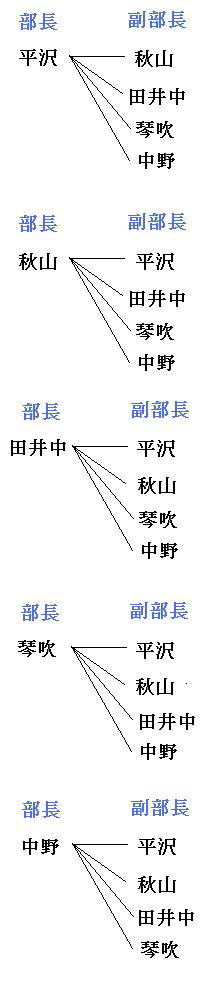
数学・算数 56人 2人組 組み合わせ 56人を2人組に分ける組み合わせは何通りですか? 計算方法もお願いします 質問No 目の出方は何通りですか。 問題2:赤青2つのサイコロをふりました。目の出方は何通りですか。 問題3:大きさも形も色も同じサイコロを2つ同時にふりました。目の出方は何通りですか? いかがでしょうか。答えは、問題1と2が36通りで、問題3が21通りです。小学6年生の算数 場合の数|組み合わせ 練習問題プリント ツイート 順序は考えず選んで組を作るときの選び方 「組み合わせ」を調べる方法を練習できる問題プリントです。 場合の数・組み合わせ(1) 答え 場合の数・組み合わせ(2) 答え 場合
算数 組み合わせ 何通りのギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素 | 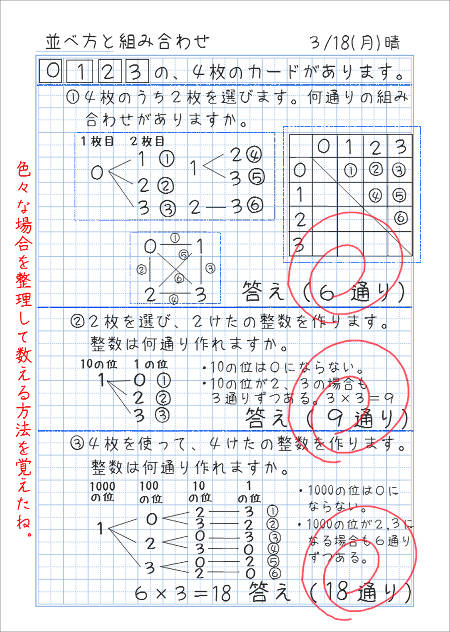 算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素 | 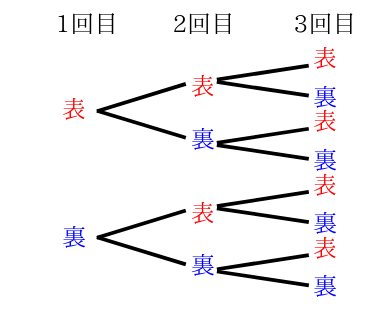 算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素 |
 算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素 | 算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素 | 算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素 |
 算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素 | 算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素 | 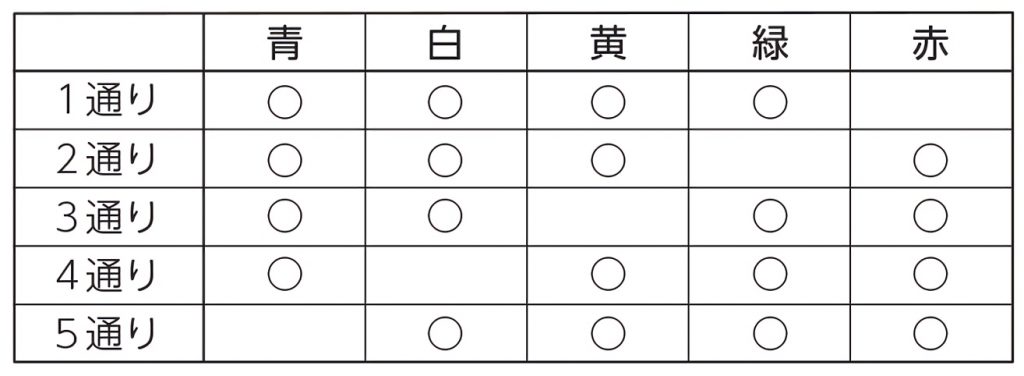 算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素 |
 算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素 |  算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素 | 算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素 |
 算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素 |  算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素 | 算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素 |
 算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素 | 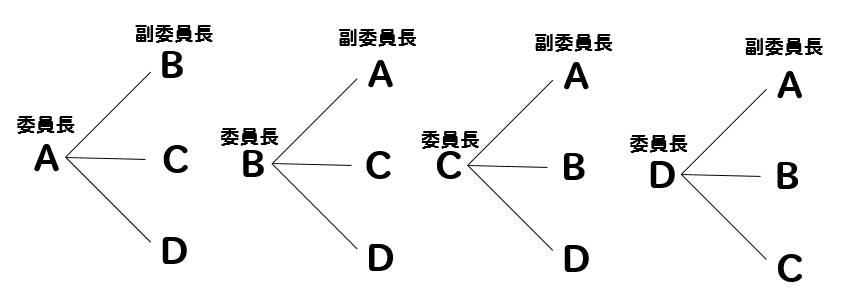 算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素 |  算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素 |
 算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素 |  算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素 |  算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素 |
算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素 |  算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素 |  算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素 |
 算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素 | 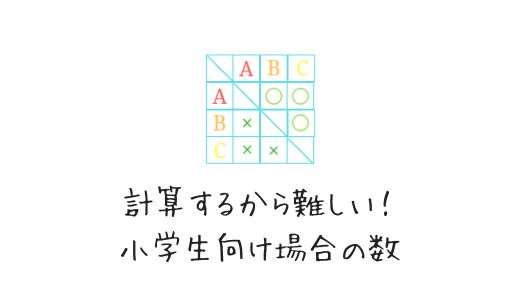 算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素 | 算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素 |
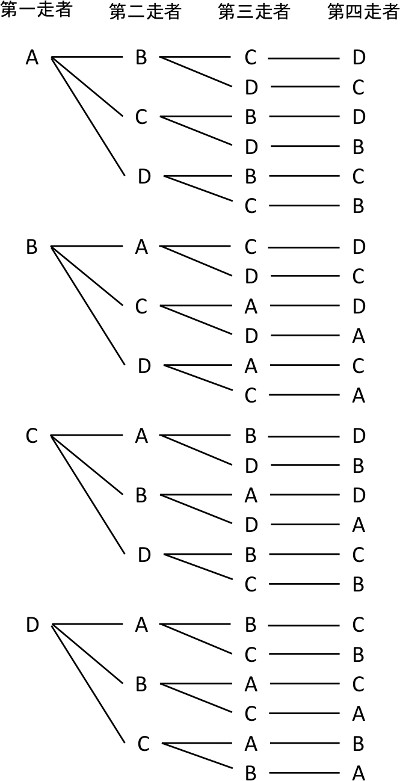 算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素 |  算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素 |  算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素 |
算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素 |  算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素 | 算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素 |
 算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素 |  算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素 | 算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素 |
算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素 |  算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素 |  算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素 |
 算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素 | 算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素 | 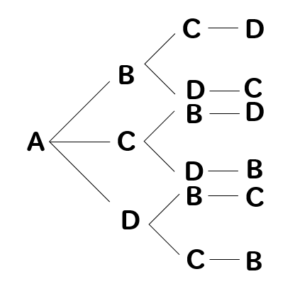 算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素 |
 算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素 |  算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素 |  算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素 |
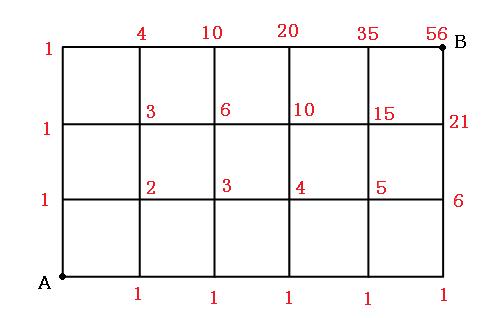 算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素 |  算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素 |  算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素 |
算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素 |  算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素 |  算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素 |
 算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素 |  算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素 | 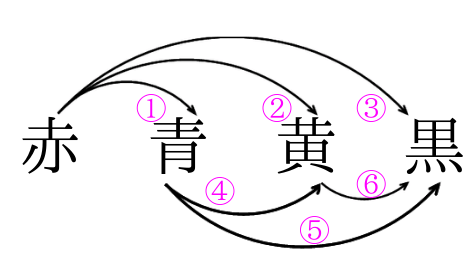 算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素 |
 算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素 |  算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素 | 算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素 |
 算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素 |  算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素 | 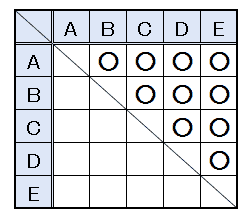 算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素 |
 算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素 | 算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素 | 算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素 |
算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素 |  算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素 |  算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素 |
 算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素 |  算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素 | 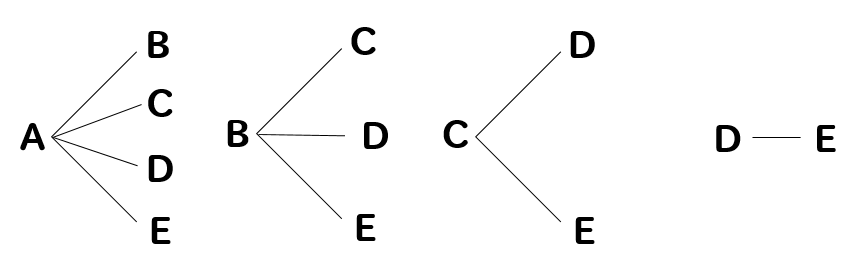 算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素 |
 算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素 |  算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素 | 算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素 |
 算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素 | 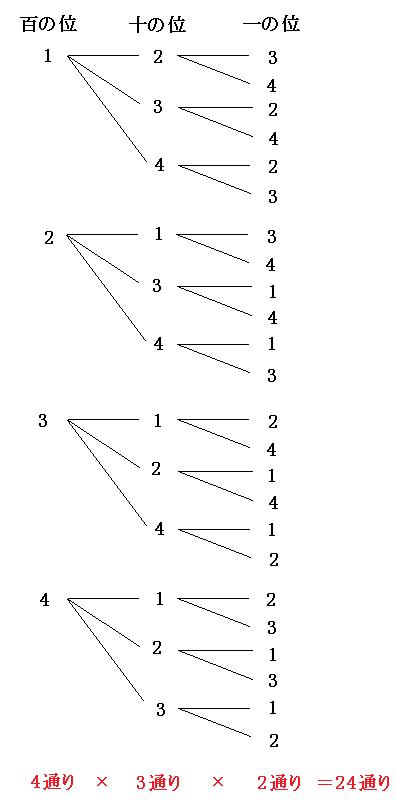 算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素 |  算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素 |
 算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素 |  算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素 |  算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素 |
 算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素 |  算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素 |  算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素 |
 算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素 | 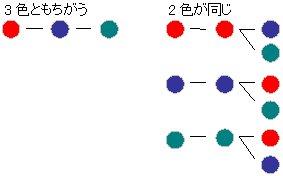 算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素 |  算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素 |
 算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素 |  算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素 |  算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素 |
 算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素 | 算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素 |  算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素 |
算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素 |  算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素 | 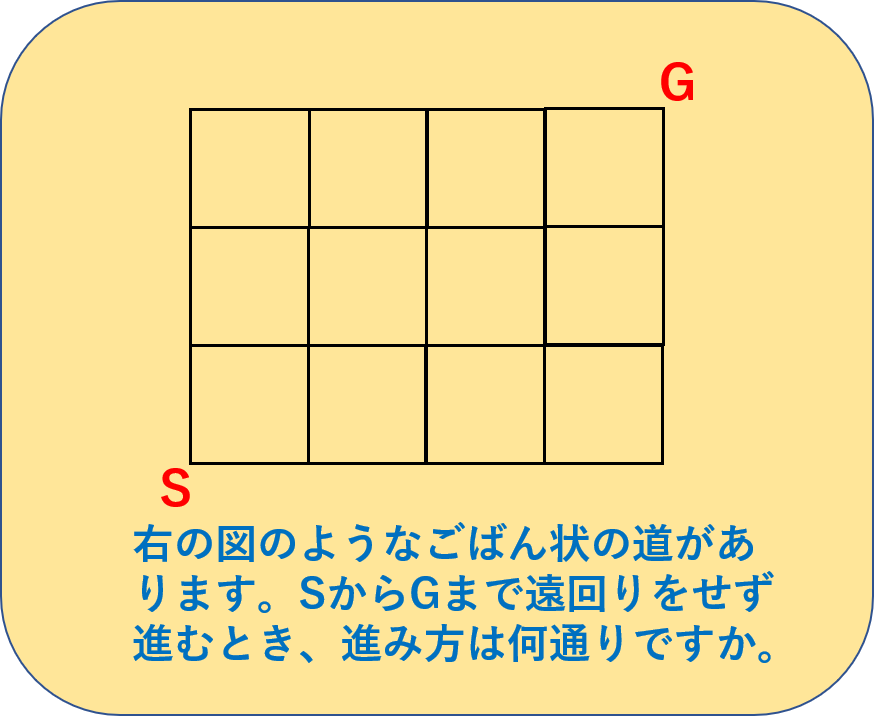 算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素 |
 算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素 |  算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素 |  算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素 |
 算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素 | 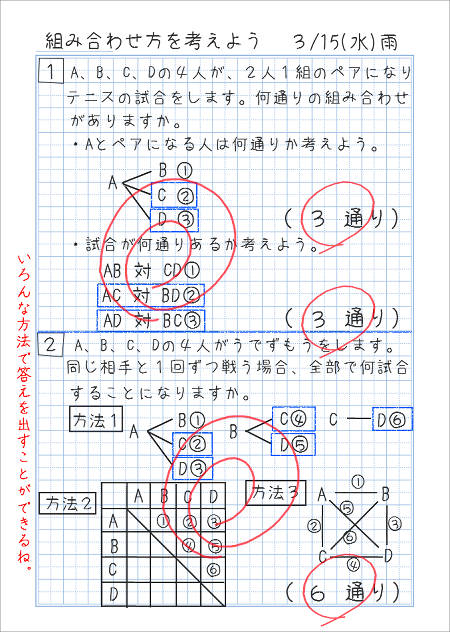 算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素 |  算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素 |
 算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素 | 算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素 | 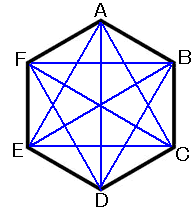 算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素 |
 算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素 |  算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素 |
あとは、右上半分を数えて6通りという事が分かります。 まとめ 今回の記事では、組み合わせの数の数え方について書いてみました。 特に計算がでてくるという訳ではないので、算数の中ではかなり異色な単元ではないでしょうか。 組み合わせの例題 5枚のくじがあります。それぞれのくじには1~5までの数字が書かれてあります。 この中から2枚を引いたとき、数字の組み合わせは何通りあるでしょうか。 力技で解いてみる まずは、力技で数えてみましょう。 小学校の算数で登場する
Incoming Term: 算数 組み合わせ 何通り,
コメント
コメントを投稿